Understanding how fast a program runs is key to writing good code. Terms like O(n), O(log n), and O(2^n) describe how algorithms scale, but they often confuse beginners. At the heart of these expressions are two simple concepts: logarithms and exponents. These mathematical tools help explain how the time or steps needed by a program grow as the input size increases.
Whether a task becomes slower or stays efficient often depends on these ideas. This article breaks down logarithms and exponents in complexity analysis, showing how they impact performance and why they matter in practical programming.
Let’s begin with logarithms. A logarithm is the reverse of an exponent. In plain terms, it answers the question: "To what power must a base number be raised to get another number?" For example, log₂(8) = 3 because 2³ = 8. In computing, logarithms often use base 2 since binary systems are built on powers of 2.
In complexity analysis, logarithmic time is considered very efficient. You’ll usually see it written as O(log n). This means that as the size of your input data grows, the number of steps your program takes grows slowly. A good example of this is binary search. Instead of checking every item one by one, it splits the dataset in half with every step, cutting down the work dramatically.
Why does this matter? Imagine searching through a phone book. A linear search would make you go through every name, one after another. But with binary search, you jump straight to the middle and decide which half to focus on next. This keeps happening until you find what you're looking for—or you know it's not there. With each step reducing the search space by half, the time it takes only grows a little, even if the list gets very large.
Another place where logarithms show up is in tree structures. In a balanced binary tree, the height of the tree is log₂(n), meaning the number of layers grows very slowly as nodes are added. Many efficient algorithms use this to their advantage when searching or sorting data.
So, when you see O(log n) in complexity analysis, it’s a good sign. It usually means the program is designed well and will scale nicely even as data grows.
Now, let's talk about exponents. If logarithmic time is efficient, exponential time is the opposite. Exponents describe functions that grow very fast. In computing, these often appear as O(2^n), O(n!), or similar formats. When you see an exponent in a complexity function, it's a warning sign. This means that the number of operations grows extremely fast with each increase in input size.
Let’s take O(2^n) as an example. This kind of complexity happens in problems like the traveling salesman problem, where you have to check every possible route. If there are 10 cities, you’re looking at 2^10 = 1024 combinations. That’s manageable. But if there are 20 cities, it jumps to over a million. The cost of solving the problem quickly becomes too high.
Another place where exponential time shows up is in recursive algorithms without optimization. If each function call leads to two more calls, and this continues with every step, the total number of calls becomes 2^n. Unless these are reduced with methods like memoization or pruning, the function can take a long time to finish.
This is why many algorithms are considered impractical when they have exponential complexity. Programmers often try to rewrite or replace them with faster approaches—often with a tradeoff in accuracy or completeness.
It’s also important to mention polynomial time here. While not exponential, some functions like O(n²) or O(n³) still involve exponents. These are more manageable, especially for small inputs, but they still get slower as data grows. Sorting algorithms like bubble sort or selection sort fall in this range. In contrast, merge sort or quick sort, which operate closer to O(n log n), are faster and more scalable.
So, understanding exponents isn’t just about theory. It directly affects how long your code will run and whether it will be useful in practice.
One of the easiest ways to see the impact of logarithms and exponents is to compare them. Let's say you have an input size of 16. A logarithmic algorithm with O(log₂ n) would take 4 steps (since log₂(16) = 4). An exponential algorithm with O(2^n) would take 65,536 steps. That’s a massive difference for the same input size.
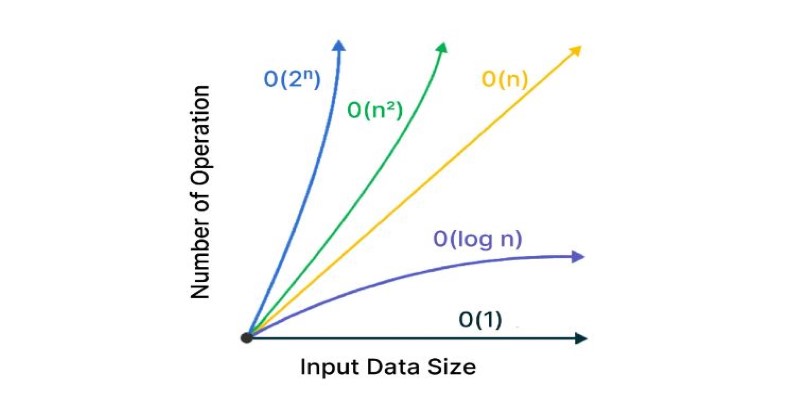
This contrast becomes even more important as n increases. While O(log n) barely grows, O(2^n) explodes. That's why engineers always aim to reduce complexity. If they can bring it down from exponential to polynomial or from polynomial to logarithmic, the improvements can be huge.
You can think of logarithmic algorithms as ones that shrink the problem at each step. Exponential ones, on the other hand, expand the problem, making it harder to handle.
In coding interviews, candidates are often asked to find ways to cut down complexity. Being able to recognize when a solution is exponential and suggesting a logarithmic or linear approach can make a big difference.
This is also why understanding the difference isn’t just helpful—it’s necessary. It shapes how software is built, how it performs, and how scalable it becomes.
Logarithms and exponents in complexity analysis play a major role in how we understand algorithm performance. Logarithmic time points to efficient, scalable solutions, while exponential time often signals slow, impractical ones. Recognizing the difference between these growth patterns helps developers write better code and avoid performance issues. Whether you're designing algorithms or preparing for technical interviews, grasping these concepts is essential. In a world of growing data and demanding applications, knowing how your code scales isn’t just helpful—it’s a core part of building smart, fast, and reliable software.

Google AI open-sourced GPipe, a neural network training library for scalable machine learning and efficient model parallelism

Stay updated with AV Bytes as it captures AI industry shifts and technological breakthroughs shaping the future. Explore how innovation, real-world impact, and human-centered AI are changing the world

Simpson’s Paradox is a statistical twist where trends reverse when data is combined, leading to misleading insights. Learn how this affects AI and real-world decisions

How self-driving tractors supervised remotely are transforming AI farming by combining automation with human oversight, making agriculture more efficient and sustainable

How to use MongoDB with Pandas, NumPy, and PyArrow in Python to store, analyze, compute, and exchange data effectively. A practical guide to combining flexible storage with fast processing

Gain control over who can access and modify your data by understanding Grant and Revoke in SQL. This guide simplifies managing database user permissions for secure and structured access

How the AI Robotics Accelerator Program is helping universities advance robotics research with funding, mentorship, and cutting-edge tools for students and faculty

Looking for the best Airflow Alternatives for Data Orchestration? Explore modern tools that simplify data pipeline management, improve scalability, and support cloud-native workflows

Find out the key differences between SQL and Python to help you choose the best language for your data projects. Learn their strengths, use cases, and how they work together effectively

Discover how DataRobot training empowers citizen data scientists with easy tools to boost data skills and workplace success

Fujitsu AI-powered biometrics revealed at Mobile World Congress 2025 claims to predict crime before it happens, combining real-time behavioral data with AI. Learn how it works, where it’s tested, and the privacy concerns it raises
How the SUMPRODUCT function in Excel can simplify your data calculations. This detailed guide explains its uses, structure, and practical benefits for smarter spreadsheet management