Ever misspelled a word in a search bar and still got exactly what you meant? Or did you notice your contact app spotting duplicates even when names aren’t spelled the same? That’s often thanks to Levenshtein Distance—a smart computer science concept that measures how different two strings of text are. It calculates the number of changes needed to turn one word into another, helping machines recognize what looks or sounds similar.

In a world where AI powers spell-check, predictive text, and recommendation engines, this simple metric plays a big role behind the scenes. In this article, we’ll break it down clearly and show why it matters in today’s AI world.

What is Levenshtein Distance?

At its simplest, Levenshtein Distance is a number that tells you how many changes you need to make to turn one word or string into another. These changes can be one of three types: insert a character, delete a character, or substitute one character for another. Each of these is considered one “edit.” The total number of edits needed is the Levenshtein Distance.

Let’s take a basic example. Say you want to change “cat” into “cut.” You only need to substitute “a” with “u.” That’s one edit, so the Levenshtein Distance is 1. Now, imagine converting “flaw” into “lawn.” That takes two edits: removing the “f” and adding an “n” at the end. Distance: 2.

The concept was developed by the Russian scientist Vladimir Levenshtein in 1965. While the idea itself is over half a century old, its usefulness has only grown. The explosion of natural language processing, machine learning, and search applications has made the metric a common tool.

Levenshtein Distance belongs to a broader group of string metric algorithms known as edit distance algorithms. While there are other forms—like Hamming Distance, which only measures substitution and assumes strings are of equal length—Levenshtein is more flexible. It accounts for additions and deletions, making it more practical in real-world applications where typos and uneven string lengths are common.

How Does It Work Behind the Scenes?

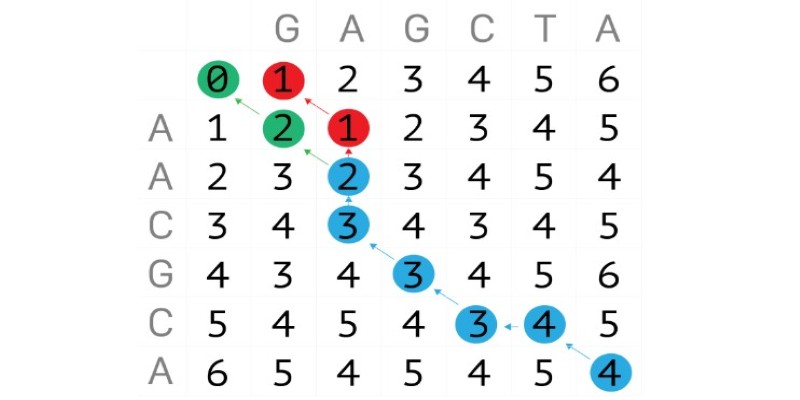
To understand how Levenshtein Distance is actually calculated, imagine a grid or matrix. One string is placed across the top, and the other string goes down the side. The algorithm fills in the grid cell by cell, calculating the minimum number of operations needed to reach each cell based on its neighboring cells.

Let’s say we’re comparing the strings “book” and “back.” Here’s the breakdown:

First, we initialize a grid of size (length of “book” + 1) x (length of “back” + 1).

Each cell keeps track of how many edits it would take to get from the beginning of one string to that point in the other.

Starting from zero edits (both strings empty), the algorithm adds costs for each insert, delete, or substitute operation as it moves through the grid.

When it gets to the last cell, it gives you the total number of edits required—that’s your Levenshtein Distance.

This grid-based technique might sound tedious, but it’s what makes the algorithm dynamic and efficient. It doesn’t just blindly count edits. It evaluates every possible path and chooses the one with the fewest total changes. That’s why it works so well, even when strings differ in length or have multiple errors.

Modern programming languages like Python, Java, and C++ often have built-in libraries or extensions (like Python’s Levenshtein module) that handle this for you, making implementation easier.

Applications in Artificial Intelligence and Data Matching

Levenshtein Distance becomes especially powerful when applied to the imperfect, unpredictable inputs found in real-world AI tasks. Its strength lies in how it helps systems handle human error—typos, misspellings, or inconsistent formatting—without losing context. In natural language processing (NLP), it's used for spell-checking, fuzzy matching, and chatbot input correction. If someone types "shw me the weather,” a chatbot can still respond correctly because the difference between “shw” and “show” is just one edit. This makes interactions smoother and more natural.

Data deduplication is another practical use. Imagine two customer entries—“Johnathan Smith” and “Jonathen Smith.” While they look slightly different, the distance between them is small enough for the system to flag them as likely duplicates. This helps maintain clean, accurate databases with minimal manual effort.

Search engines rely on it, too. When you mistype a search term, the algorithm compares your input to popular queries using Levenshtein Distance and shows the closest matches. It's what powers those handy "Did you mean?" suggestions.

In machine learning, especially with NLP models, this distance is used to score model outputs. A translation that’s close but not exact still has value, and the algorithm helps quantify that.

Its usefulness extends even further—supporting recommendation systems, fraud detection, autocomplete tools, and genetic pattern analysis. It's versatile, foundational, and still incredibly relevant.

Why Does Levenshtein Distance Still Matter Today?

Levenshtein Distance still matters because it’s simple, reliable, and highly effective—especially in today’s AI landscape. While it was introduced in the 1960s, its ability to bring clarity to messy, user-generated data remains unmatched. It helps systems understand typos, match strings, and process imperfect input with grace. Unlike complex black-box models, Levenshtein Distance is easy to explain and visualize, making it a transparent tool for developers and analysts alike.

Even with the rise of powerful language models like GPT and Claude, this algorithm hasn’t been replaced—it's often used alongside them. Tasks like data cleaning, fuzzy matching, and training set alignment to benefit from their accuracy and simplicity. It also scales well thanks to modern optimizations, allowing efficient use even in large datasets. In a world of cutting-edge AI, Levenshtein Distance remains a quiet but essential foundation. It just works—no hype is needed.

Conclusion

Levenshtein Distance continues to play a crucial role in AI and data systems by making machines more tolerant, accurate, and context-aware. Its ability to handle imperfections—like typos or small differences in text—makes it a trusted tool in everything from chatbots to search engines. Despite its age, it remains relevant because it’s simple, interpretable, and effective. As AI evolves, foundational tools like this stay essential, quietly supporting the systems we use every day without demanding attention.